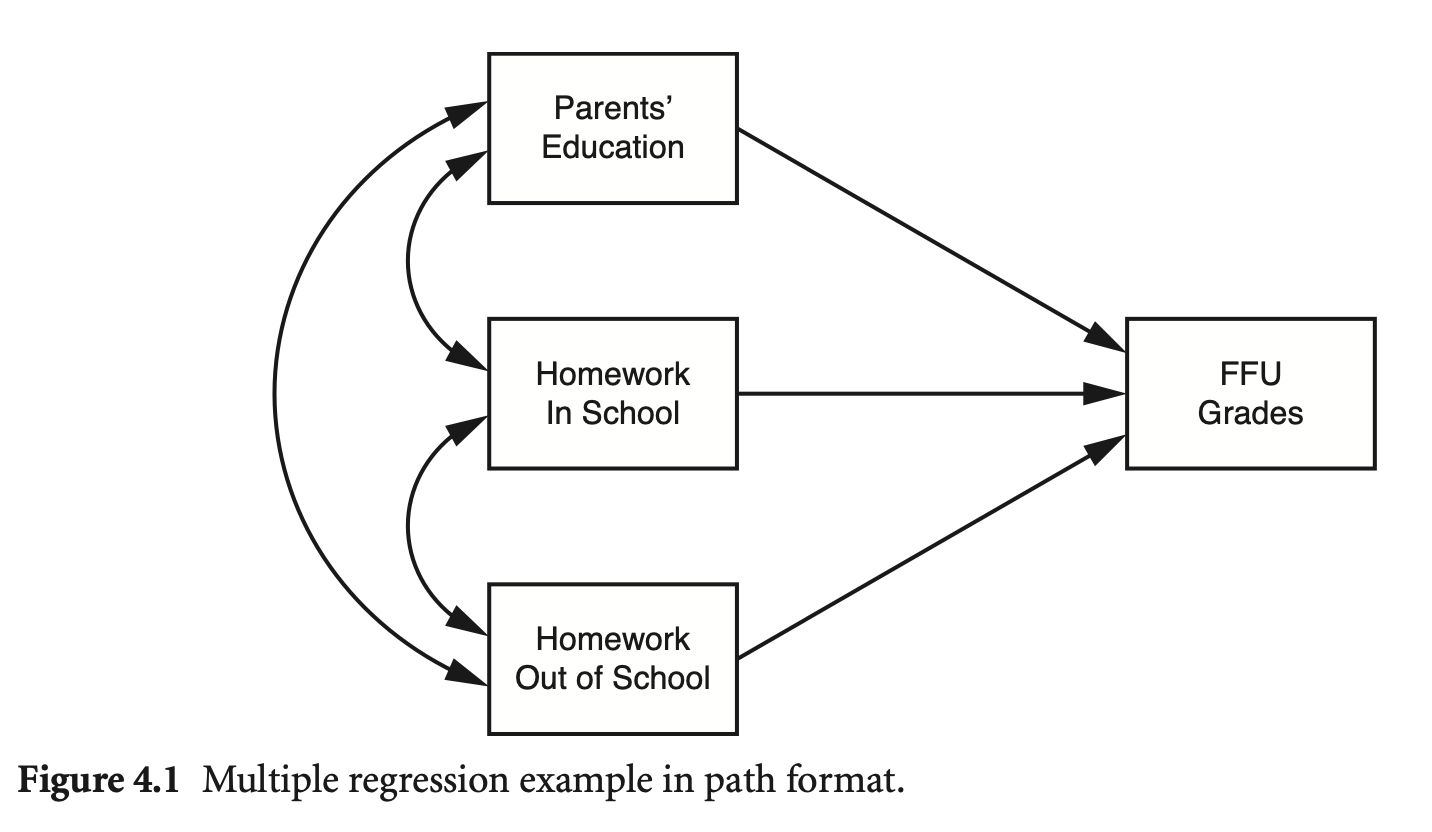
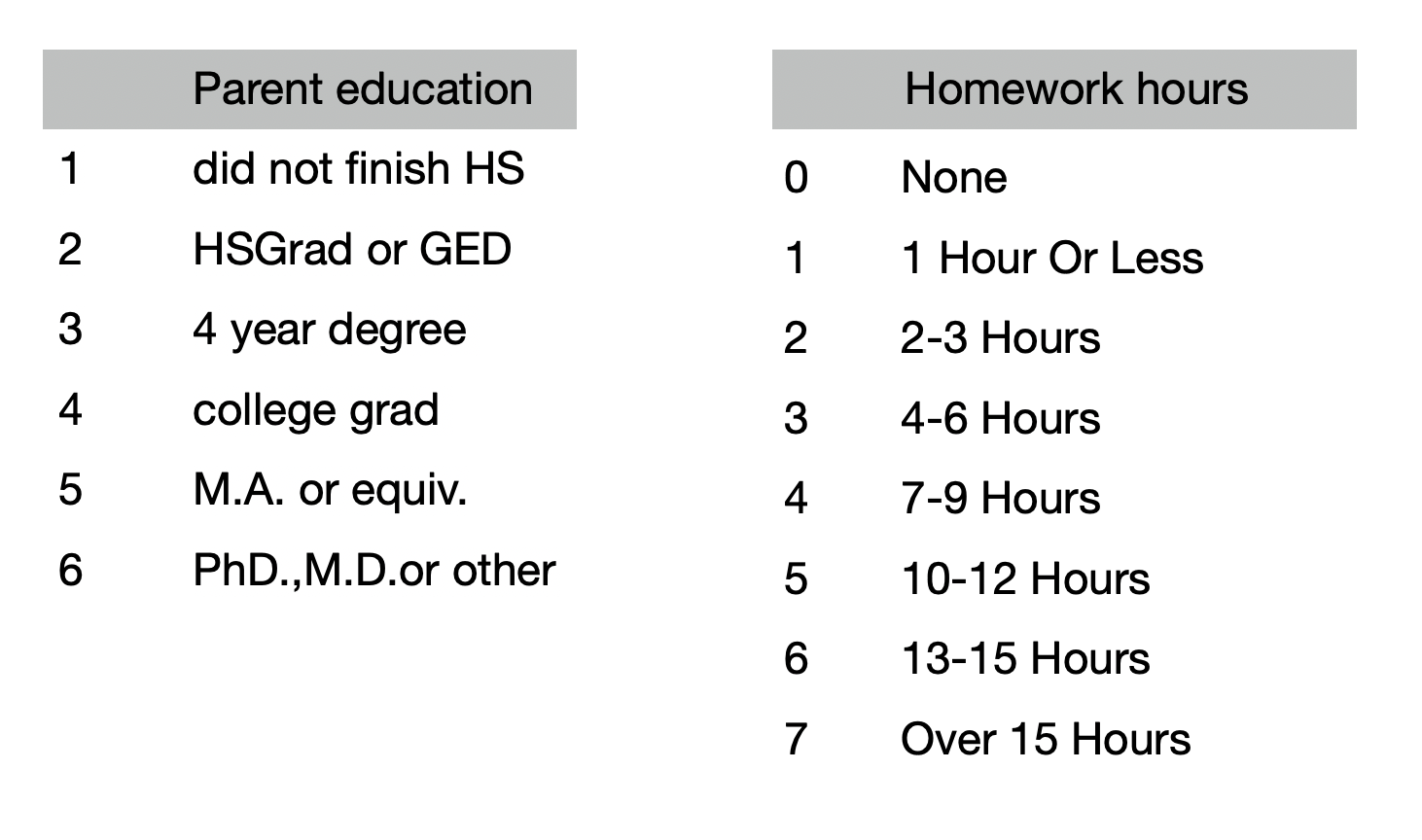
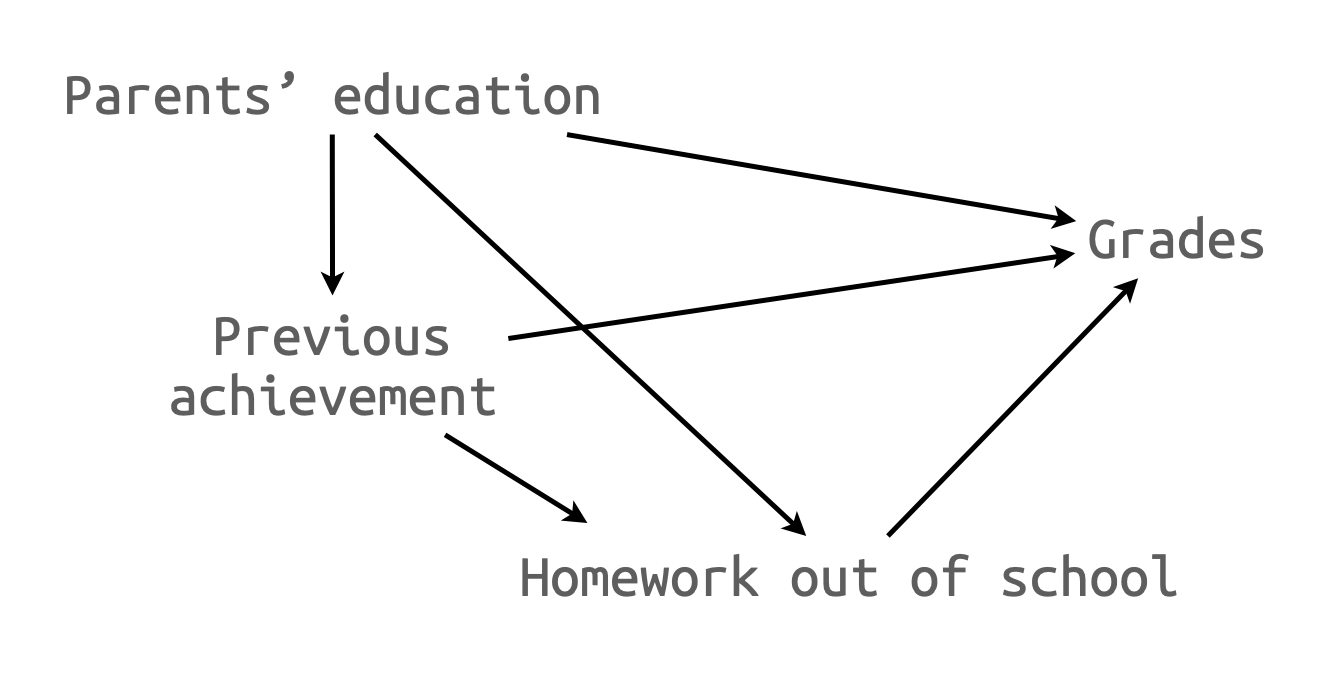
National Education Longitudinal Study of 1988 (NELS:88)
Source: p.69 in Multiple Regression and Beyond (3e) by Timothy Z. Keith
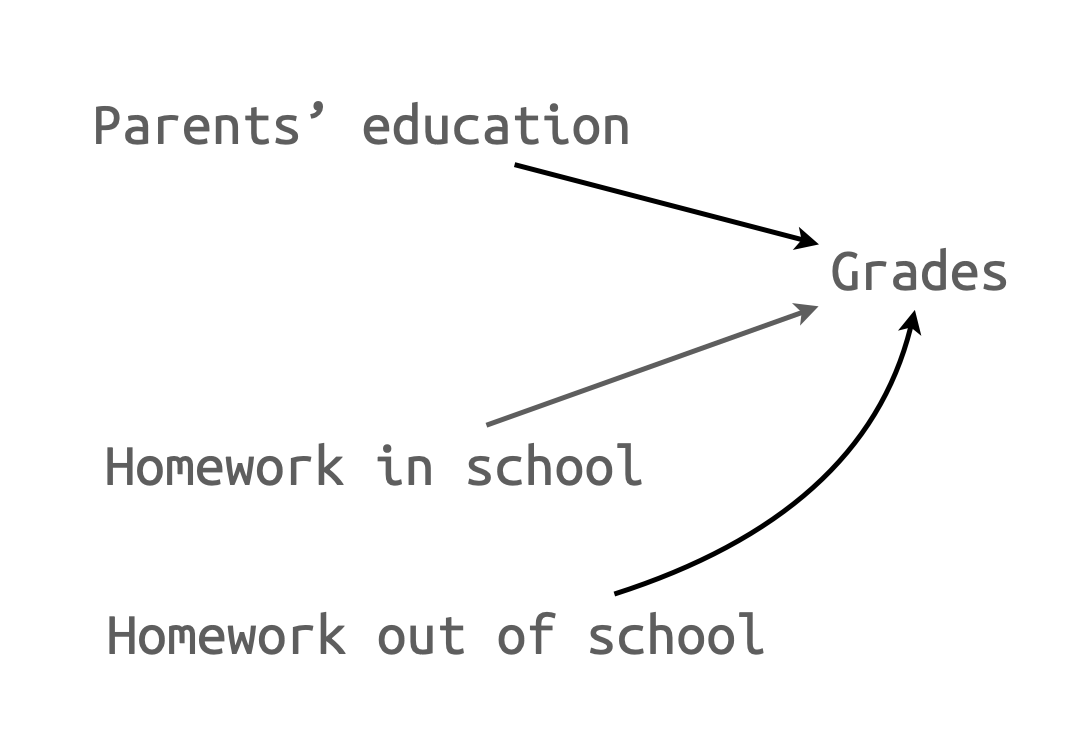
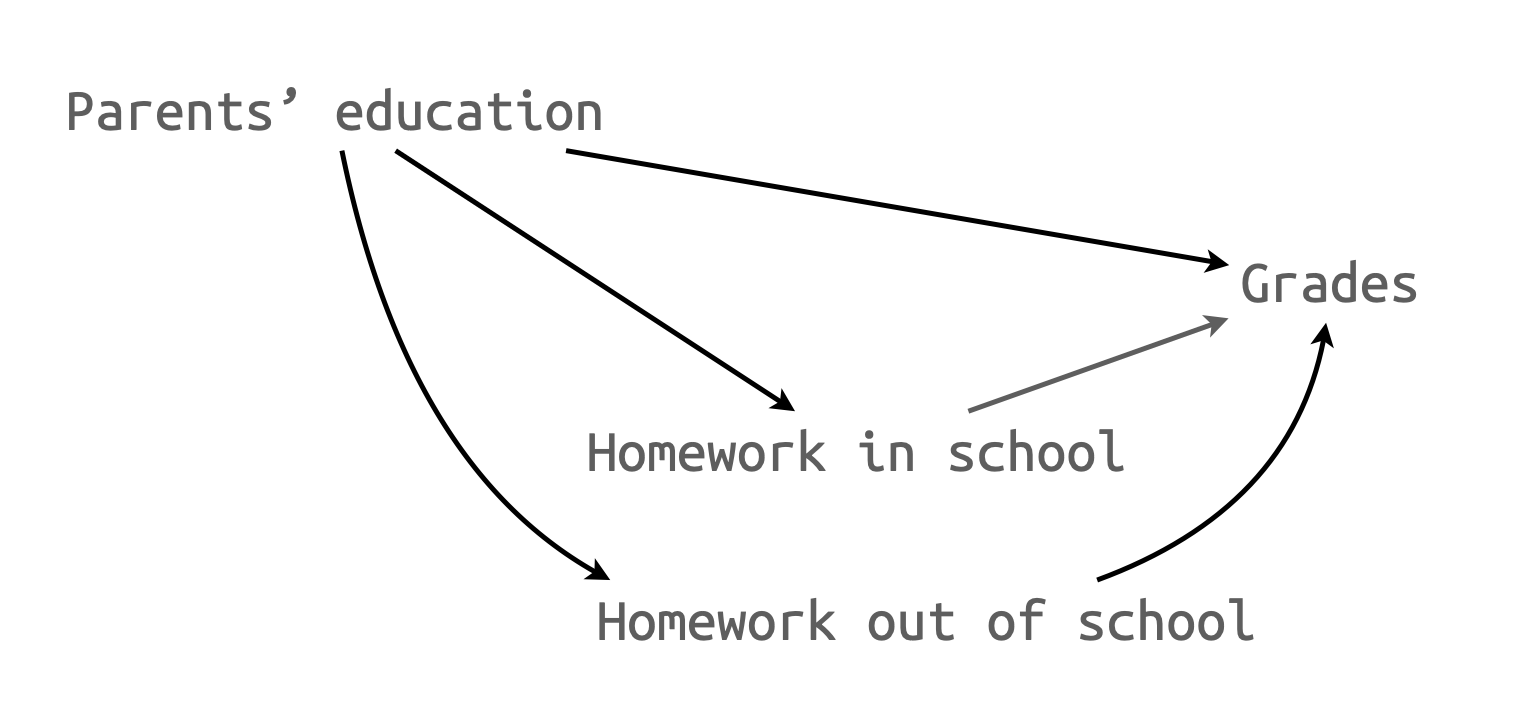
연구주제: 학생들의 과제는 성적에 영향을 주는가? 준다면 그 영향력의 크기는 어떠한가? 데이터 NELS88 sample.csv
grades: 10학년의 성적 평균 in English, Math, Science, Social Studies.pared: 부모의 교육 수준 (높은 쪽)hw_in, hw_out: 10학년 때 학생들이 보고한 숙제하는데 보낸 주당 평균 시간 (in school or out of school)
<- read_csv ("data/nels88_sample_4_11.csv" )<- nels |> select (grades = ffugrad, pared = bypared, hw_in = f1s36a1, hw_out = f1s36a2, prev = bytests)
# A tibble: 300 × 5
grades pared hw_in hw_out prev
<dbl> <dbl> <dbl> <dbl> <dbl>
1 4.33 3 1 0 56.4
2 8 5 1 2 58.4
3 6.5 4 0 2 44.4
4 7.33 6 3 2 67.4
5 6 2 3 2 50.7
6 4 3 1 NA 46.0
7 6.5 6 1 7 62.4
8 4.33 2 1 2 46.0
9 3.5 2 3 1 46.3
10 6.5 3 7 5 62.4
# ℹ 290 more rows
# summarize data summary (nels)
grades pared hw_in hw_out
Min. :1.333 Min. :1.000 Min. :0.000 Min. :0.000
1st Qu.:4.500 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:1.000
Median :5.750 Median :3.000 Median :2.000 Median :2.000
Mean :5.610 Mean :3.197 Mean :2.135 Mean :2.554
3rd Qu.:6.750 3rd Qu.:4.000 3rd Qu.:3.000 3rd Qu.:4.000
Max. :8.000 Max. :6.000 Max. :7.000 Max. :7.000
NA's :20 NA's :25 NA's :24
prev
Min. :29.34
1st Qu.:43.79
Median :50.81
Mean :50.86
3rd Qu.:57.06
Max. :69.96
NA's :12
# count values |> count (pared)
# A tibble: 6 × 2
pared n
<dbl> <int>
1 1 31
2 2 47
3 3 123
4 4 53
5 5 23
6 6 23
# A tibble: 9 × 2
hw_out n
<dbl> <int>
1 0 17
2 1 75
3 2 78
4 3 31
5 4 33
6 5 17
7 6 11
8 7 14
9 NA 24
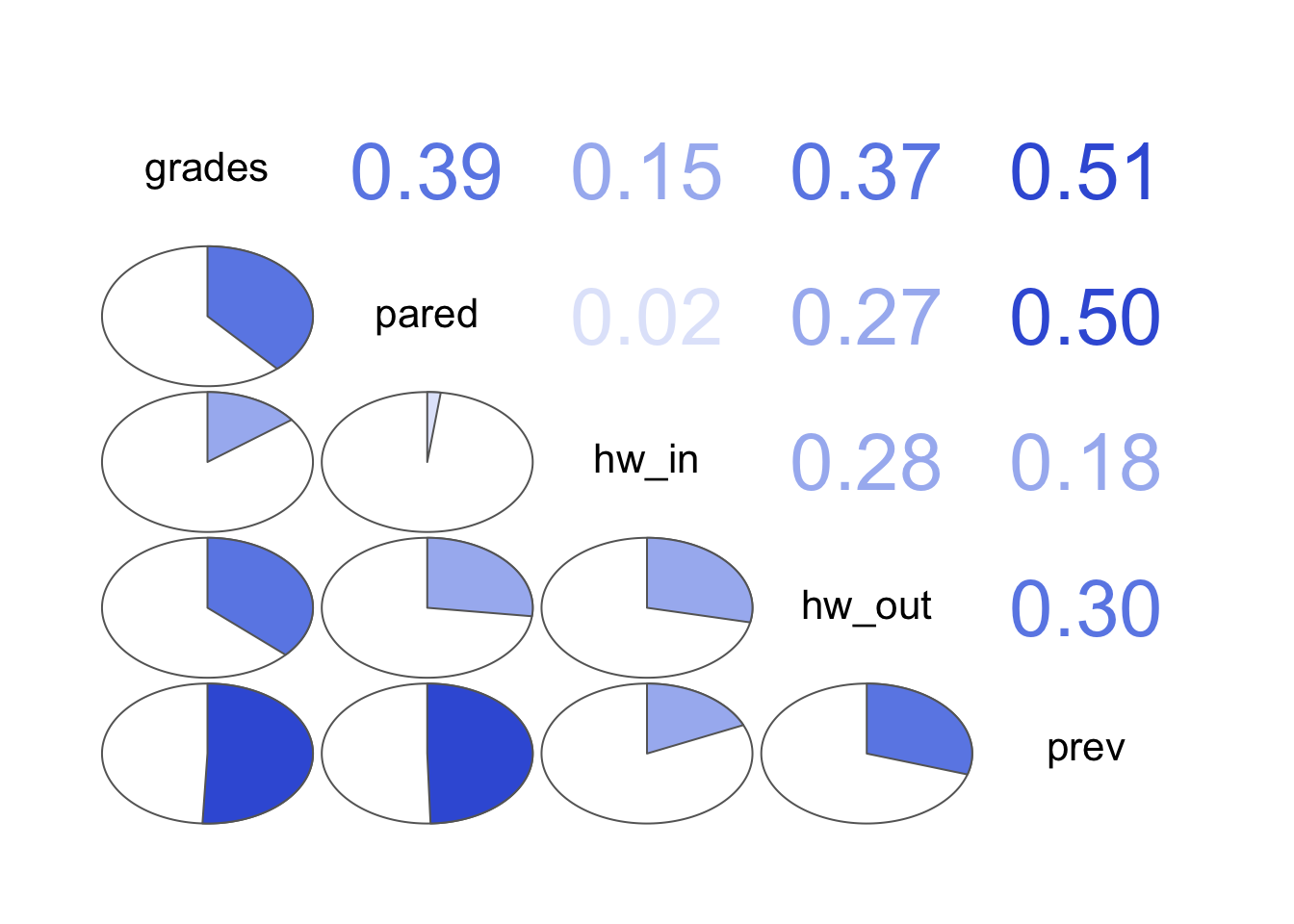
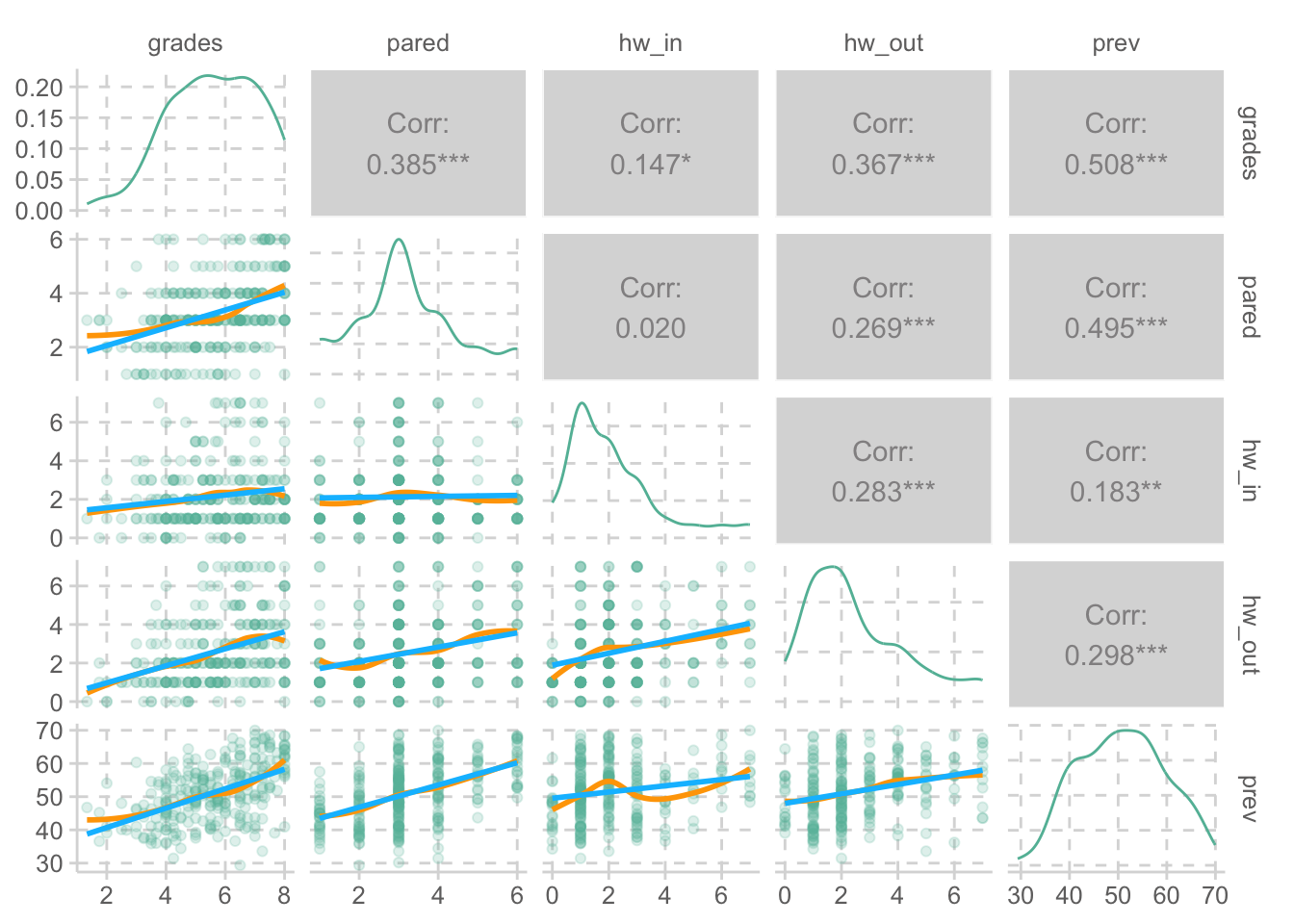
변수들 간의 관계 탐색 lowerCor (nels)library (corrgram)|> corrgram (upper.panel = panel.cor, lower.panel = panel.pie)
grads pared hw_in hw_ot prev
grades 1.00
pared 0.39 1.00
hw_in 0.15 0.02 1.00
hw_out 0.37 0.27 0.28 1.00
prev 0.51 0.50 0.18 0.30 1.00
<- function (data, mapping, ...){ggplot (data = data, mapping = mapping) + geom_point (alpha = .2 ) + geom_smooth (method = loess, se = FALSE , color = "orange" , ...) + geom_smooth (method = lm, se = FALSE , color = "deepskyblue" , ...)<- function (data, ...) {:: ggpairs (data, lower = list (continuous = trendlines))
세 개의 독립변수로 예측
B1. 인과모형 A: 부분 회귀 계수들
<- lm (grades ~ pared + hw_in + hw_out, data = nels)summary (mod1)
Call:
lm(formula = grades ~ pared + hw_in + hw_out, data = nels)
Residuals:
Min 1Q Median 3Q Max
-3.5760 -0.9737 0.1006 0.9497 2.8618
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.76892 0.24369 15.466 < 2e-16 ***
pared 0.36326 0.06365 5.707 3.13e-08 ***
hw_in 0.05066 0.05014 1.010 0.313
hw_out 0.22884 0.04752 4.816 2.49e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.299 on 260 degrees of freedom
(36 observations deleted due to missingness)
Multiple R-squared: 0.2377, Adjusted R-squared: 0.2289
F-statistic: 27.02 on 3 and 260 DF, p-value: 3.032e-15
<- lm (hw_out ~ pared, data = nels)summary (mod2)
Call:
lm(formula = hw_out ~ pared, data = nels)
Residuals:
Min 1Q Median 3Q Max
-2.8260 -1.4548 -0.4548 1.1740 5.2874
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.34143 0.28227 4.752 3.25e-06 ***
pared 0.37114 0.08016 4.630 5.66e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.746 on 274 degrees of freedom
(24 observations deleted due to missingness)
Multiple R-squared: 0.07255, Adjusted R-squared: 0.06917
F-statistic: 21.44 on 1 and 274 DF, p-value: 5.658e-06
D: 표준화 계수 및 부분 상관 계수
# beta: standardized coefficients :: lm.beta (mod1) |> print () # 범주형 변수가 있을 때는 사용하지 말것!
Call:
lm(formula = grades ~ pared + hw_in + hw_out, data = nels)
Standardized Coefficients::
(Intercept) pared hw_in hw_out
NA 0.31961944 0.05707121 0.28071933
summ (mod1, part.corr= TRUE , model.info= FALSE , model.fit= FALSE ) |> print ()
Standard errors: OLS
--------------------------------------------------------------------
Est. S.E. t val. p partial.r part.r
----------------- ------ ------ -------- ------ ----------- --------
(Intercept) 3.77 0.24 15.47 0.00
pared 0.36 0.06 5.71 0.00 0.33 0.31
hw_in 0.05 0.05 1.01 0.31 0.06 0.05
hw_out 0.23 0.05 4.82 0.00 0.29 0.26
--------------------------------------------------------------------
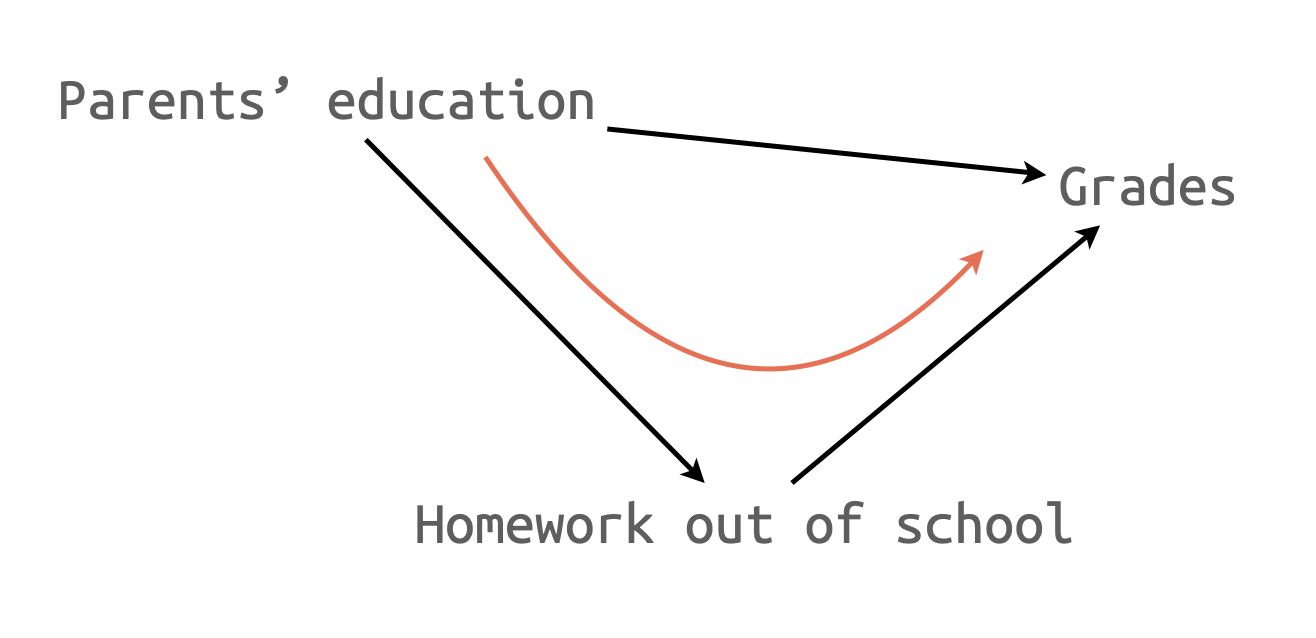
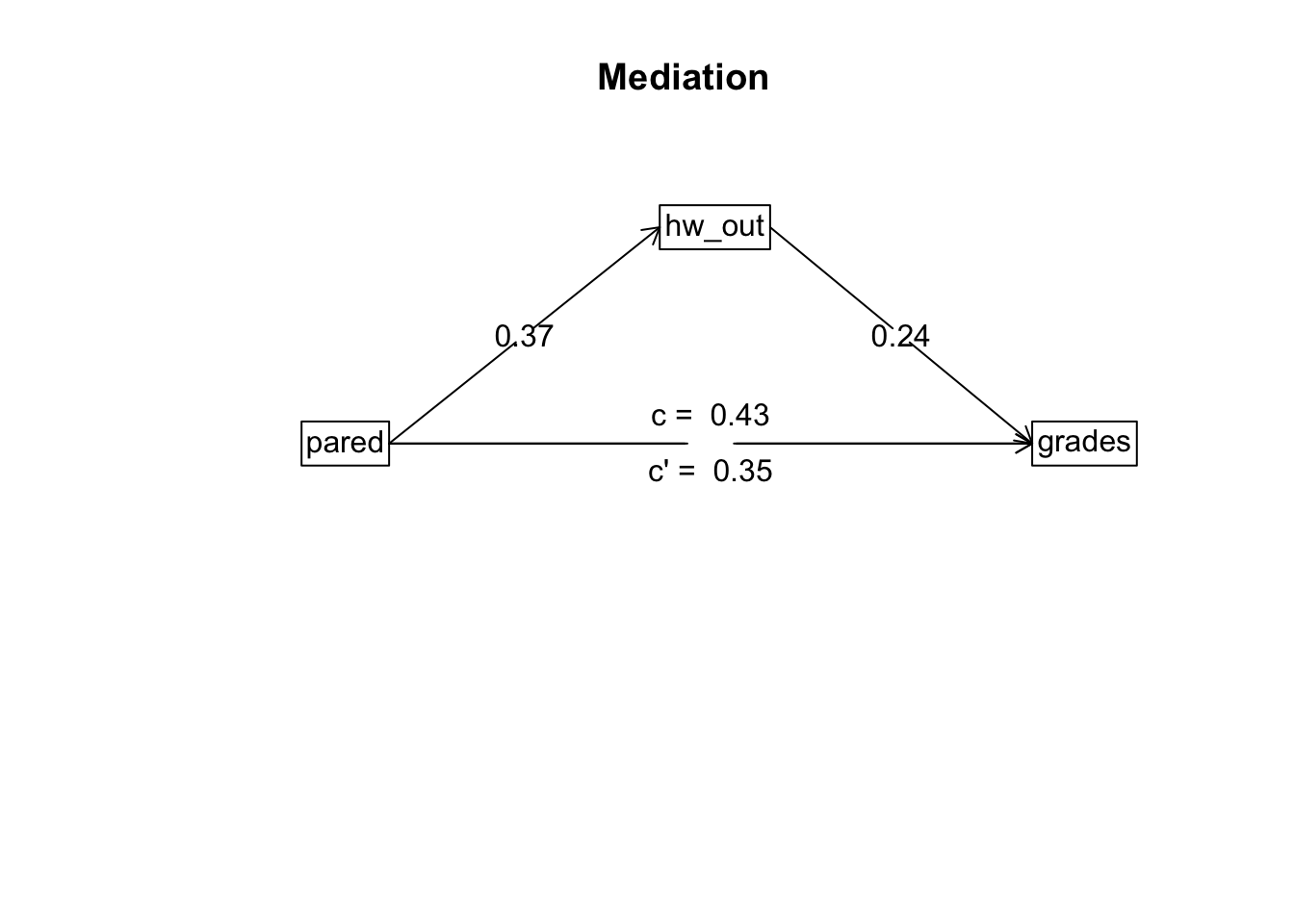
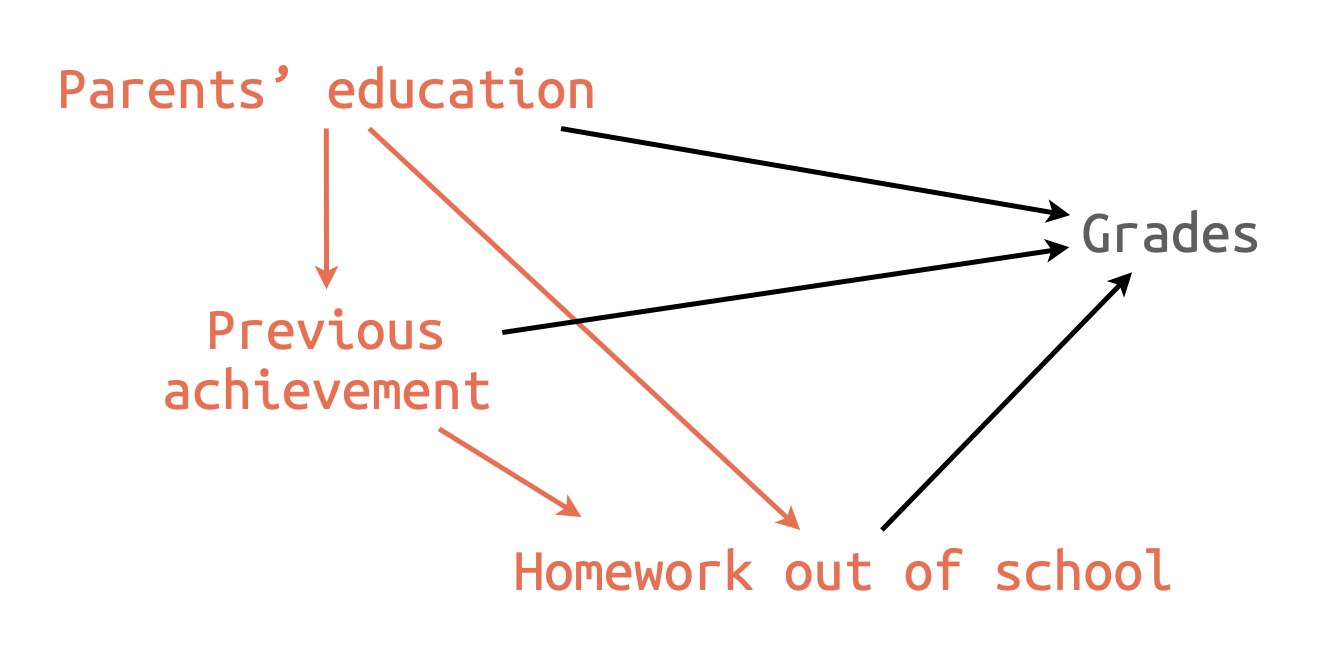
E: 간접효과의 크기와 검증
summary (mediate (grades ~ pared + (hw_out), data = nels))
Call: mediate(y = grades ~ pared + (hw_out), data = nels)
Direct effect estimates (traditional regression) (c') X + M on Y
grades se t df Prob
Intercept 3.90 0.21 18.39 297 6.04e-51
pared 0.35 0.06 5.66 297 3.61e-08
hw_out 0.24 0.04 5.33 297 1.90e-07
R = 0.47 R2 = 0.22 F = 41.42 on 2 and 297 DF p-value: 1.36e-16
Total effect estimates (c) (X on Y)
grades se t df Prob
Intercept 4.22 0.21 19.85 298 1.78e-56
pared 0.43 0.06 7.06 298 1.20e-11
'a' effect estimates (X on M)
hw_out se t df Prob
Intercept 1.36 0.27 5.10 298 6.09e-07
pared 0.37 0.08 4.85 298 2.00e-06
'b' effect estimates (M on Y controlling for X)
grades se t df Prob
hw_out 0.24 0.04 5.33 297 1.9e-07
'ab' effect estimates (through all mediators)
grades boot sd lower upper
pared 0.09 0.09 0.03 0.04 0.14
변수의 추가: 4개의 독립변수로 예측
B2. 인과모형 B: 부분 회귀 계수들
<- lm (grades ~ pared + hw_out, data = nels)<- lm (grades ~ pared + hw_out + prev, data = nels)
F: 모형의 비교
export_summs (mod3, mod4, error_format = "({p.value})" ) |> print ()
────────────────────────────────────────────────────
Model 1 Model 2
───────────────────────────────────
(Intercept) 3.80 *** 0.94 *
(0.00) (0.05)
pared 0.37 *** 0.20 **
(0.00) (0.00)
hw_out 0.24 *** 0.17 ***
(0.00) (0.00)
prev 0.07 ***
(0.00)
───────────────────────────────────
N 270 258
R2 0.23 0.35
────────────────────────────────────────────────────
*** p < 0.001; ** p < 0.01; * p < 0.05.
Column names: names, Model 1, Model 2
G: 표준화 계수 및 부분 상관 계수
# beta: standardized coefficients :: lm.beta (mod4) |> print () # 범주형 변수가 있을 때는 사용하지 말것!
Call:
lm(formula = grades ~ pared + hw_out + prev, data = nels)
Standardized Coefficients::
(Intercept) pared hw_out prev
NA 0.1723538 0.2039104 0.3867412
summ (mod4, part.corr= TRUE , model.info= FALSE , model.fit= FALSE ) |> print ()
Standard errors: OLS
--------------------------------------------------------------------
Est. S.E. t val. p partial.r part.r
----------------- ------ ------ -------- ------ ----------- --------
(Intercept) 0.94 0.48 1.97 0.05
pared 0.20 0.07 2.96 0.00 0.18 0.15
hw_out 0.17 0.05 3.81 0.00 0.23 0.19
prev 0.07 0.01 6.61 0.00 0.38 0.33
--------------------------------------------------------------------
추가 분석
H: Howework에 영향을 주는 요소들 분석
<- lm (hw_out ~ pared, data = nels)<- lm (hw_out ~ pared + prev, data = nels)export_summs (mod5, mod6, error_format = "({p.value})" ) |> print ()
────────────────────────────────────────────────────
Model 1 Model 2
───────────────────────────────────
(Intercept) 1.34 *** -0.51
(0.00) (0.43)
pared 0.37 *** 0.25 **
(0.00) (0.01)
prev 0.04 **
(0.00)
───────────────────────────────────
N 276 264
R2 0.07 0.12
────────────────────────────────────────────────────
*** p < 0.001; ** p < 0.01; * p < 0.05.
Column names: names, Model 1, Model 2
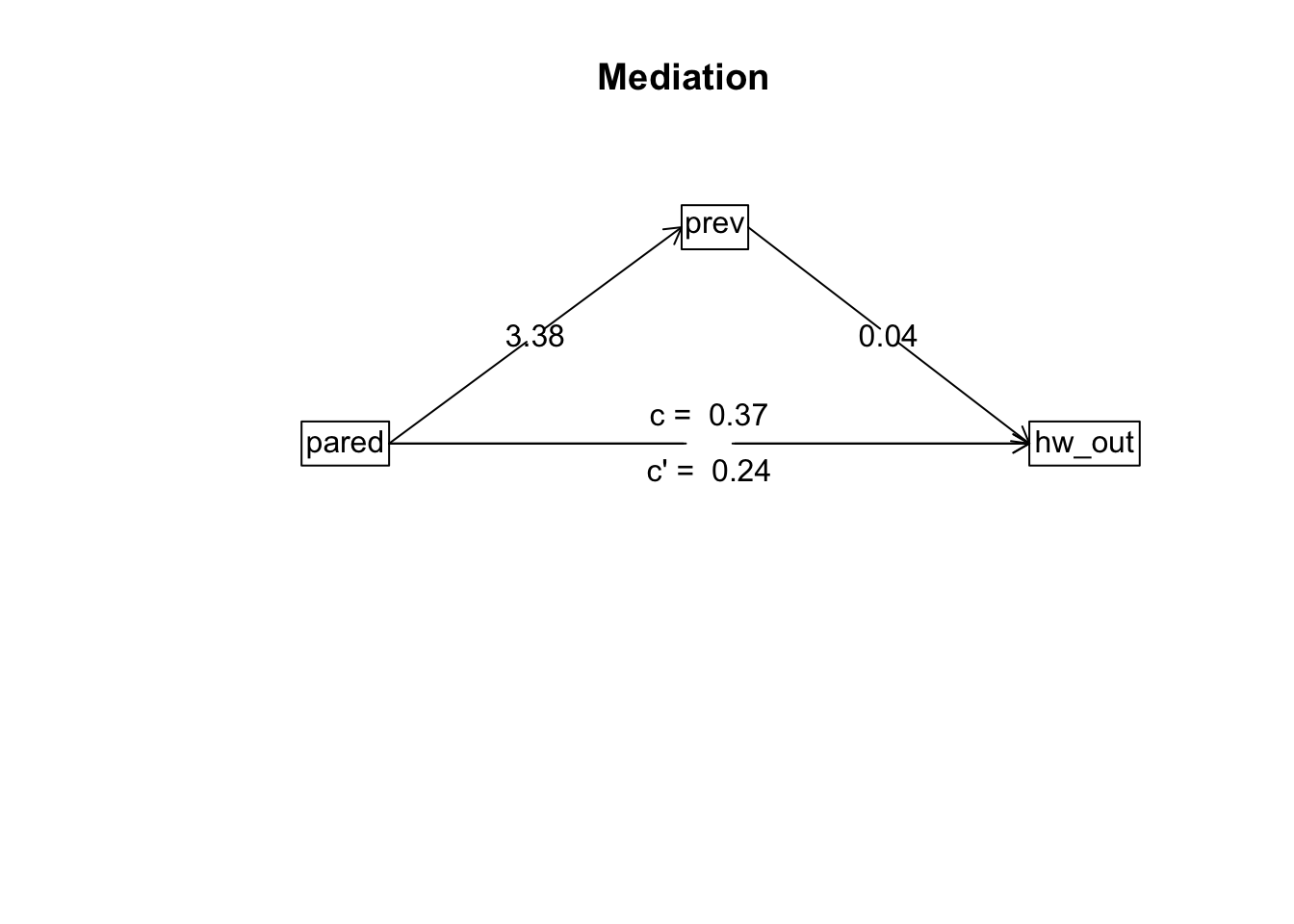
summary (mediate (hw_out ~ pared + (prev), data = nels))
Call: mediate(y = hw_out ~ pared + (prev), data = nels)
Direct effect estimates (traditional regression) (c') X + M on Y
hw_out se t df Prob
Intercept -0.25 0.58 -0.43 297 0.66600
pared 0.24 0.09 2.72 297 0.00694
prev 0.04 0.01 3.11 297 0.00202
R = 0.32 R2 = 0.1 F = 16.95 on 2 and 297 DF p-value: 1.07e-07
Total effect estimates (c) (X on Y)
hw_out se t df Prob
Intercept 1.36 0.27 5.10 298 6.09e-07
pared 0.37 0.08 4.85 298 2.00e-06
'a' effect estimates (X on M)
prev se t df Prob
Intercept 40.05 1.18 33.95 298 2.01e-104
pared 3.38 0.34 9.90 298 3.75e-20
'b' effect estimates (M on Y controlling for X)
hw_out se t df Prob
prev 0.04 0.01 3.11 297 0.00202
'ab' effect estimates (through all mediators)
hw_out boot sd lower upper
pared 0.14 0.13 0.05 0.04 0.23
위의 결과는 다음과 같은 경로분석 프레임에서 동시에 구현할 수 있으나,
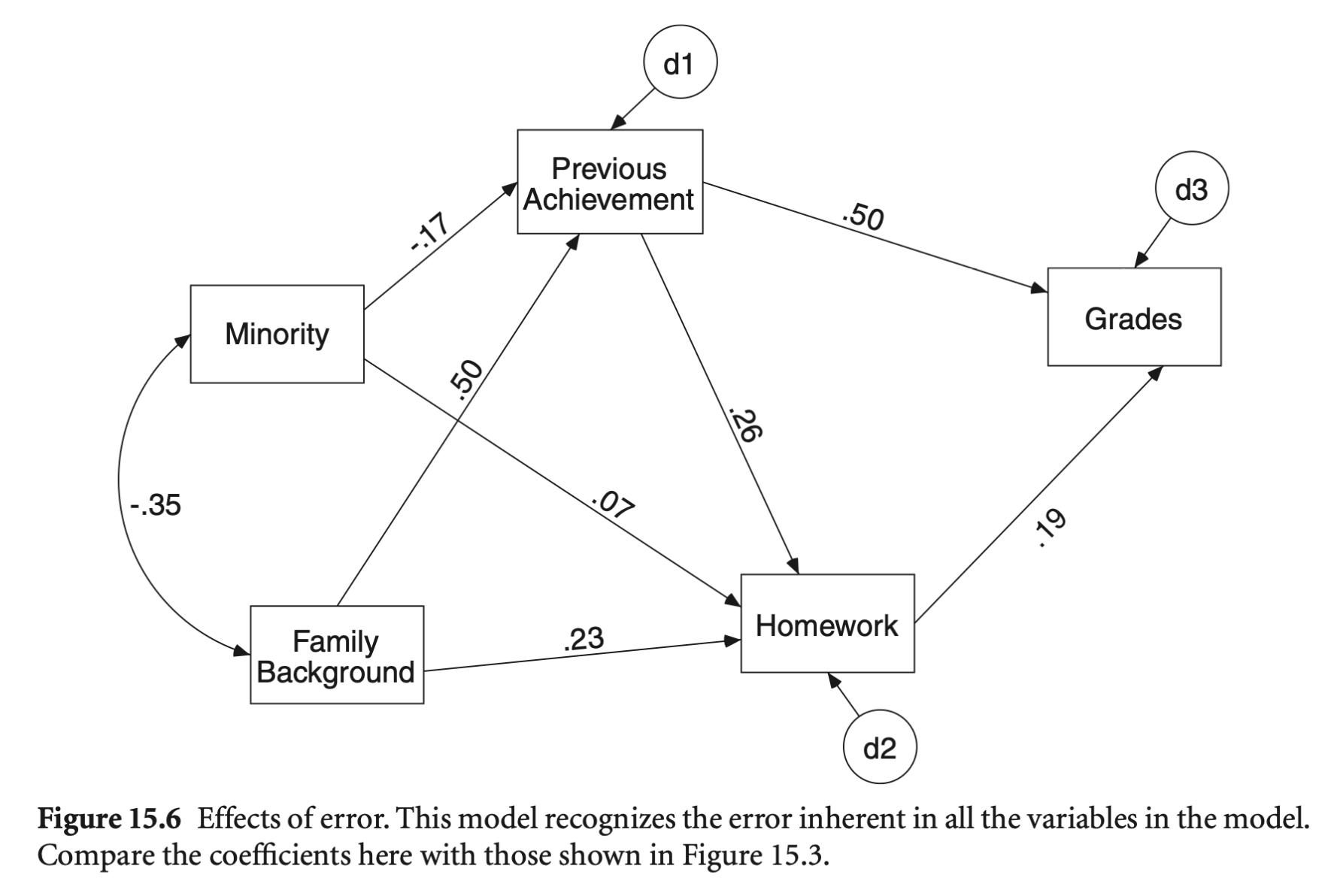
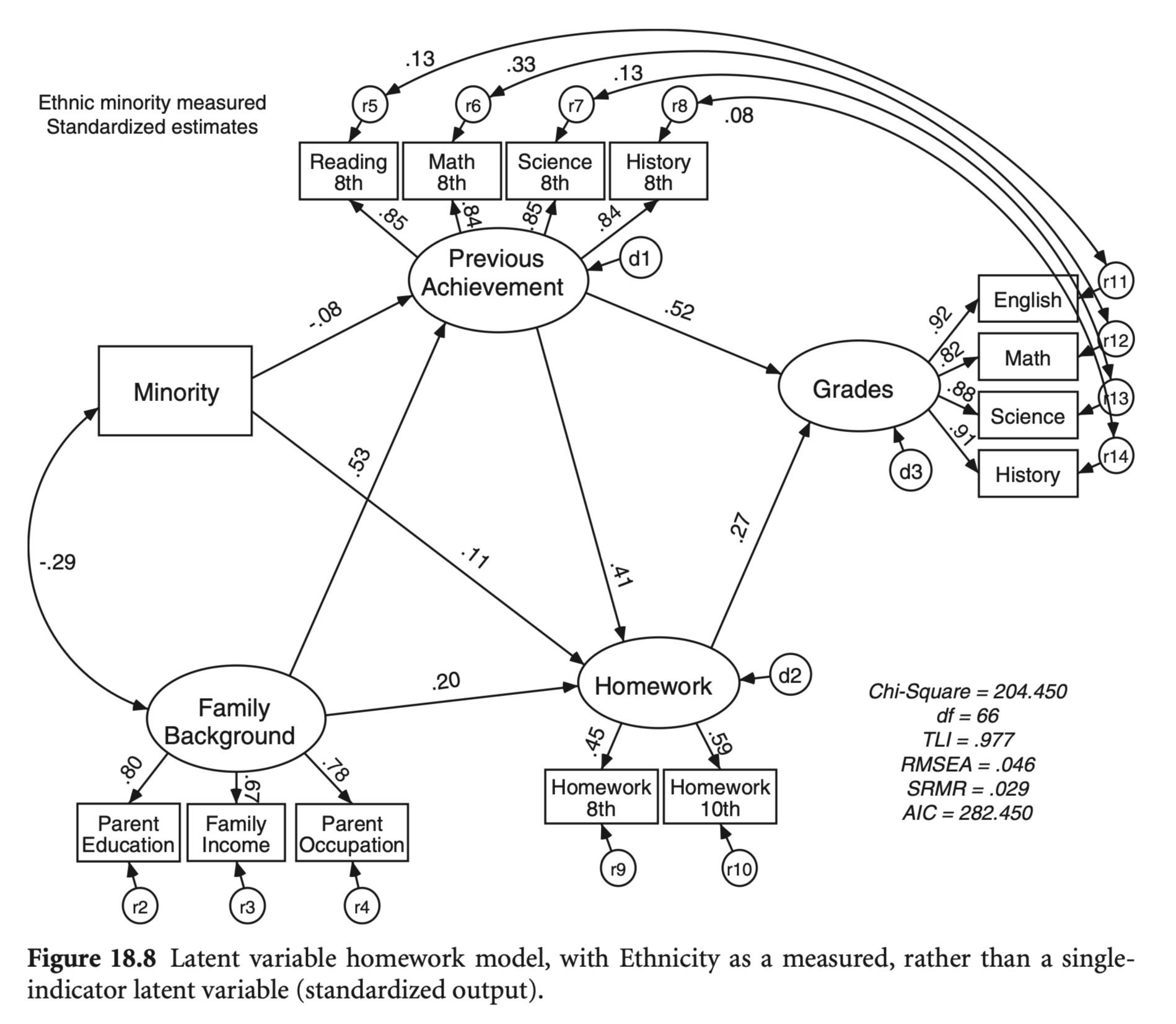
SEM (Structural Equation Modeling)의 예시
Source: p. 339, p. 421 in Multiple Regression and Beyond (3e) by Timothy Z. Keith